PIH - ch8 2/2 - Functional parsers

PIH - ch8 2/2 - Functional parsers - exercises

by @ardumont on 14 Apr 2013

Here is the second part of the exercises from the chapter 8. For the first part, go hereo.

Efficiency

Explain why the final simplification of the grammar for arithmetic expressions has a dramatic effect on the efficiency of the resulting parser.

Hint: Begin by considering how an expression comprising a single number would be parsed if this step had not been made.

We will try and parse a string with only one number to parse, "9" for example.

With this grammar:

expr   ::= expr + expr | expr - expr | term
term   ::= term * term | term / term | factor
factor ::= (expr) | nat
nat    ::= 0 | 1 | ... |

The resulting parsing with the tryout and failures is:

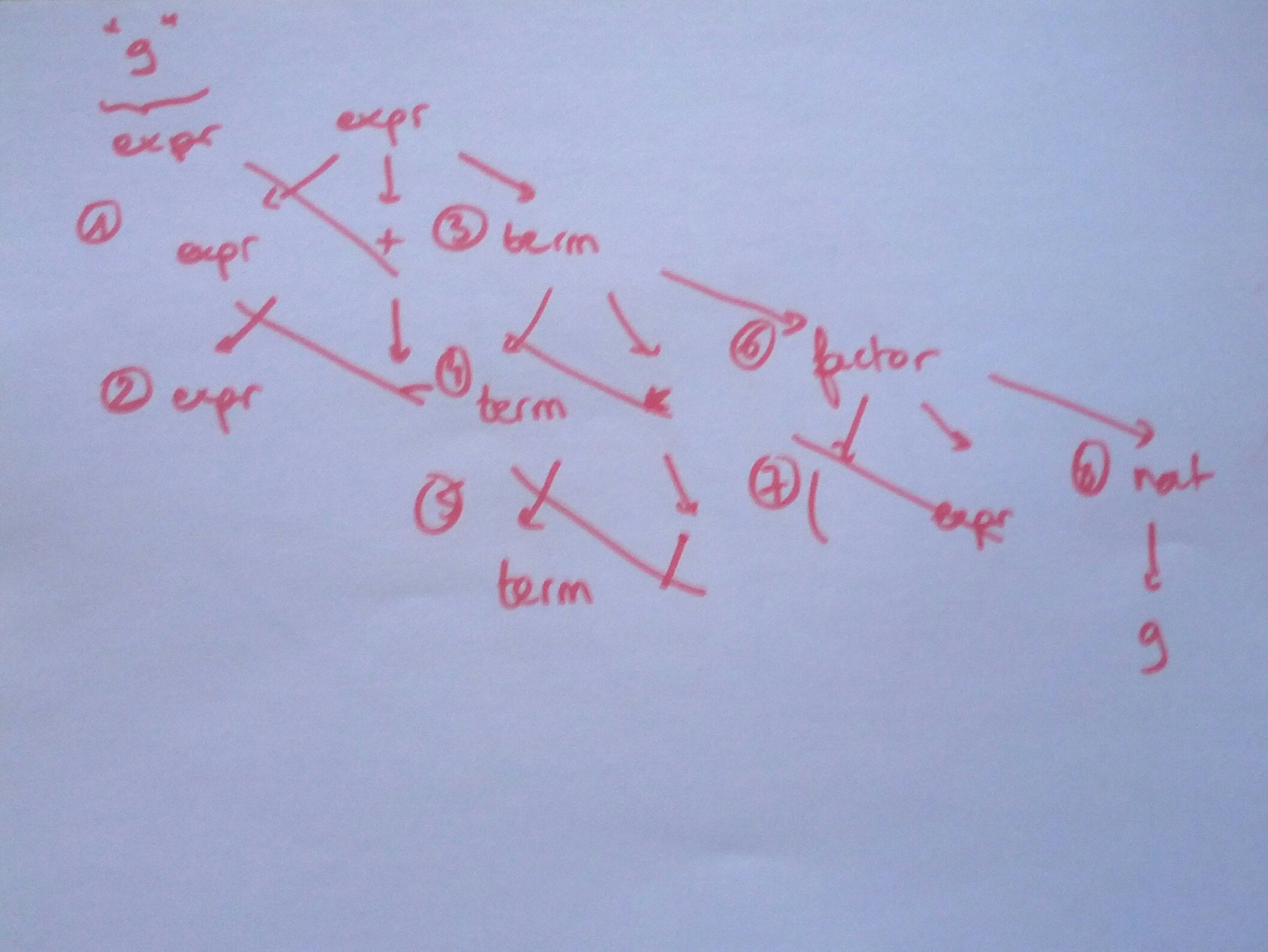
For each step, recognise the right term in the grammar, will parse and fail each possible definition until finding the rightmost (and rightful) definition:

trying and fail expr + expr, same with expr - expr, trying and succeed term
trying and fail term * term, same with term / term, trying and succeed factor
trying and fail (expr), trying and succeed nat
resolve to the right natural

With this factorised grammar:

expr   ::= term (+ expr | - expr | epsilon)
term   ::= factor (* term | / term | epsilon)
factor ::= (expr) | nat
nat    ::= 0 | 1 | ... |

The resulting parsing tree is a lot smaller because of less tryout and failtures:

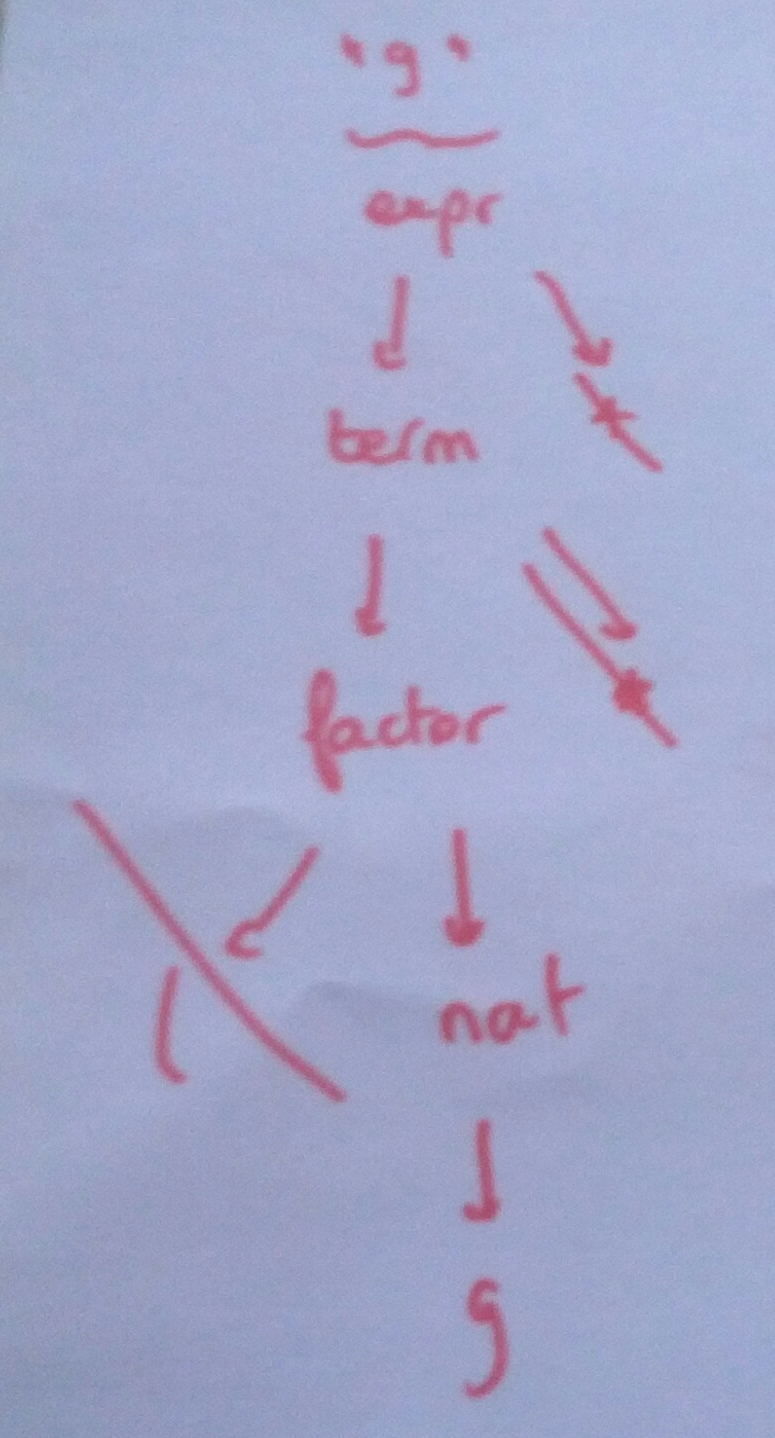
For each step, we try to parse right term in grammar, then the next symbol and fail, thus the first term parsed is the right one, no need to continue.

So with the first grammar, the efficiency of parsing will be proportional on the expression's size. With the second left-factorized grammar, the parsing is reduced.

Complete parser 1/2

Extend the parser for arithmetic expressions to support subtraction and division, based upon the following extensions to the grammar:

Grammar:

expr ::= term (+ expr | − expr | epsilon)
term ::= factor (∗ term | / term | epsilon)

Implementation:

expr :: Parser Int
expr = do t <- term
          do symbol "+"
             e <- expr
             return (t + e)
             +++ do symbol "-"
                    e <- expr
                    return (t - e)
                 +++ return t

term :: Parser Int
term = do f <- factor
          do symbol "*"
             t <- term
             return (t * f)
             +++ do symbol "/"
                    t <- term
                    return (t `div` f)
                    +++ return f

Examples:

*Parsers> eval "1+2/3"
2
*Parsers> eval "(1+2)/3"
1
*Parsers> eval "1+(2/3)"
2
*Parsers> eval "1+(2*3)"
7
*Parsers> eval "1+2*3"
7
*Parsers> eval "1+2*3-3"
4
*Parsers> eval "1+2/3-3"
-1

Complete parser 2/2

Further extend the grammar and parser for arithmetic expressions to support exponentiation, which is assumed to associate to the right and have higher priority than multiplication and division, but lower priority than parentheses and numbers. For example, 2 ↑ 3 ∗ 4 means (2 ↑ 3) ∗ 4.

Hint: The new level of priority requires a new rule in the grammar.

new grammar

Remark: The grammar's operator precedence follows the declaration order.

As:

this new rule is of lesser priority than the parenthesis precedence but greater than '*' or '/', we place this new rule in between.
the exponentiation associates to the right.

Here is the result:

expr   ::= term (+ expr | - expr | epsilon)
term   ::= factor (* term | / term | epsilon)
factor ::= exp (^ factor | epsilon)
exp    ::= (expr) | nat
nat    ::= 0 | 1 | ... |

implementation

factor :: Parser Int
factor = do e <- expo
            do symbol "^"
               f <- factor
               return (e ^ f)
               +++ return e

expo :: Parser Int
expo = do symbol "("
          e <- expr
          symbol ")"
          return e
          +++ natural

Examples:

*Parsers> eval "2^3*4"
32
*Parsers> eval "(2^3)*4"
32
*Parsers> eval "2^(3*4)"
4096

Grammar

Consider expressions built up from natural numbers using a subtraction operator that is assumed to associate to the left.

Natural

Define a natural grammar for such expressions.

expr ::= expr - nat | nat
nat  ::= 0 | 1 | ...

Implementation

Translate this grammar into a parser expr :: Parser Int.

expr :: Parser Int
expr = do e <- expr
          symbol "-"
          n <- natural
          return (e - n)
          +++ natural

Problem

What is the problem with this parser?

It loops until the stack blows.

*Parsers> parse expr "1-2"
***Exception: stack overflow

Fix

Show how it can be fixed.

Hint: Rewrite the parser using the repetition primitive many and the library function foldl.

Here is the remainder of the many parser, for a more exhaustive list, see the previous article:

many :: Parser a -> Parser [a]
many p = many1 p +++ return []

many1 :: Parser a -> Parser [a]
many1 p = do v  <- p
             vs <- many p
             return (v:vs)

Simply stated:

we parse the first expression as natural
then as long as there is a couple of - followed by a natural, we extract those values as list
then we execute the substraction using foldl with n as accumulator and ns as list and inject it into the world of parser via the return call.

expr :: Parser Int
expr = do n <- natural
          ns <- many (do symbol "-"
                         natural)
          return (foldl (-) n ns)

Examples:

*Parsers> parse expr "1-2"
[(-1,"")]
*Parsers> parse expr "1-2-3"
[(-4,"")]
*Parsers> parse expr "1-2-3-5"
[(-9,"")]
*Parsers> parse expr "1-2-3-506"
[(-510,"")]