PIH - ch8 1/2 - Functional parsers

PIH - ch8 1/2 - Functional parsers - exercises

by @ardumont on 13 Apr 2013

Before being able to fool around on this chapter, here are some pre-requisites:

import Control.Monad
import Data.Char(isDigit, isUpper, isLower, isAlpha, isAlphaNum, isSpace)

newtype Parser a  =  P (String -> [(a,String)])

parse             :: Parser a -> String -> [(a,String)]
parse (P p) inp   =  p inp

instance Monad Parser where
  -- return parser: always succeeds by returning the result value
  -- v without consuming the input
    return v      =  P (\inp -> [(v,inp)])

  -- bind
    p >>= f       =  P (\inp -> case parse p inp of
                       []        -> []
                       [(v,out)] -> parse (f v) out)

instance MonadPlus Parser where
  -- fail
    mzero         =  P (\_ -> [])
  -- choice
    p `mplus` q   =  P (\inp -> case parse p inp of
                       []        -> parse q inp
                       [(v,out)] -> [(v,out)])

I will not enter into much detail here because monads will be presented later.

As always, you'll find the sources on github.

int :: Parser Int

The library file also defines a parser int :: Parser Int for an integer. Without looking at this definition, define int.

Hint: an integer is either a minus symbol followed by a natural number, or a natural number.

The functions I will use to solve the problem:

many :: Parser a -> Parser [a]
many p = many1 p +++ return []

many1 :: Parser a -> Parser [a]
many1 p = do v  <- p
             vs <- many p
             return (v:vs)

sat :: (Char -> Bool) -> Parser Char
sat p = do x <- item; if p x then return x else Parsers.fail

nat :: Parser Int
nat = do xs <- many1 digit
         return (read xs)

space :: Parser ()
space = do many (sat isSpace)
           return ()

token :: Parser a -> Parser a
token p = do space
             x <- p
             space
             return x

natural :: Parser Int
natural = token nat

string :: String -> Parser String
string [] = return []
string (x:xs) = do char x
                   string xs
                   return (x:xs)

symbol :: String -> Parser String
symbol s = token (string s)

I have a 'choice' between parsing a negative natural number (beginning with '-') or a positive natural number.

int :: Parser Int
int = do symbol "-"
         n <- natural
         return (-n)
         +++ natural

Examples:

*Parsers> parse int "-1"
[(-1,"")]
*Parsers> parse int "-10"
[(-10,"")]
*Parsers> parse int "-101"
[(-101,"")]
*Parsers> parse int "101"
[(101,"")]
*Parsers> parse int " - 101"
[(-101,"")]

comment :: Parser ()

Define a parser comment :: Parser () for ordinary Haskell comments that begin with the symbol – and extend to the end of the current line, which is represented by the control character ’\n’.

Here are the functions I will use to answer the question:

char :: Char -> Parser Char
char x = sat (== x)

alphanum :: Parser Char
alphanum = sat isAlphaNum

Here is a first naive approach where you specify the characters you can read:

comment :: Parser ()
comment = do symbol "--"
             many (alphanum +++ char ' ')
             char '\n'
             return ()

*Parsers> parse comment "--ignoredcomment\nnotignored"
[((),"notignored")]
*Parsers> parse comment "--ignored   comment till\nnotignored"
[((),"notignored")]
*Parsers> parse comment "--42 ignoredcomment till\nnotignored"
[((),"notignored")]

Indeed, for some edge cases, this won't work:

*Parsers> parse comment "-- comment!@# that breaks\nnotignored"
[]

A simpler and better approach would be to parse anything that's not the ending control char '\n':

comment :: Parser ()
comment = do symbol "--"
             many (sat (/= '\n'))
             char '\n'
             return ()

*Parsers> parse comment "--comment!@# doesnotbreak\nnotignored"
[((),"notignored")]

Draw Tree 1/2

Using our second grammar for arithmetic expressions, draw the two possible parse trees for the expression 2 + 3 + 4.

The grammar:

expr   ::= expr + expr | term
term   ::= term * term | factor
factor ::= (expr) | nat
nat    ::= 0 | 1 | ... |

2+3+4 can be read in 2 ways:

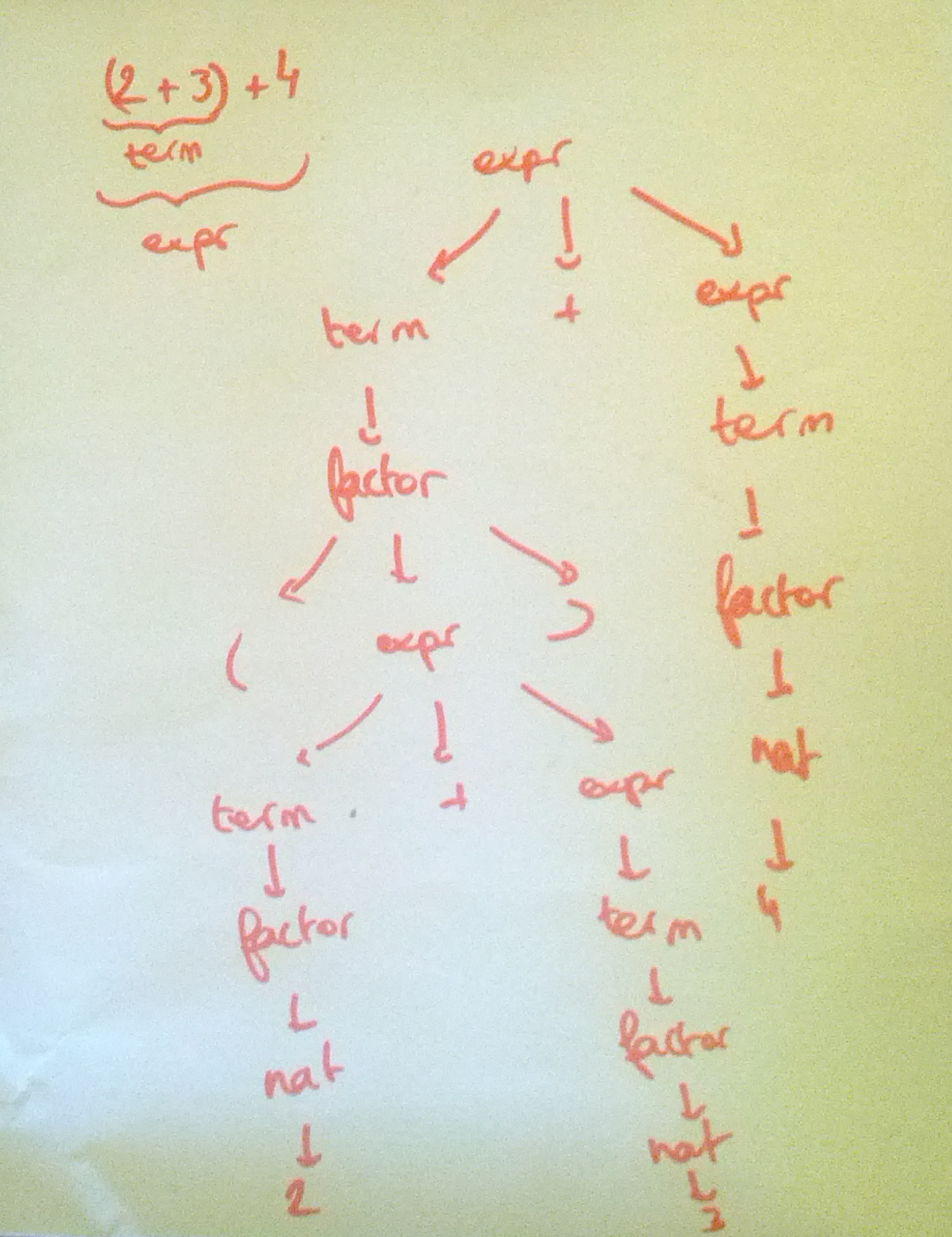
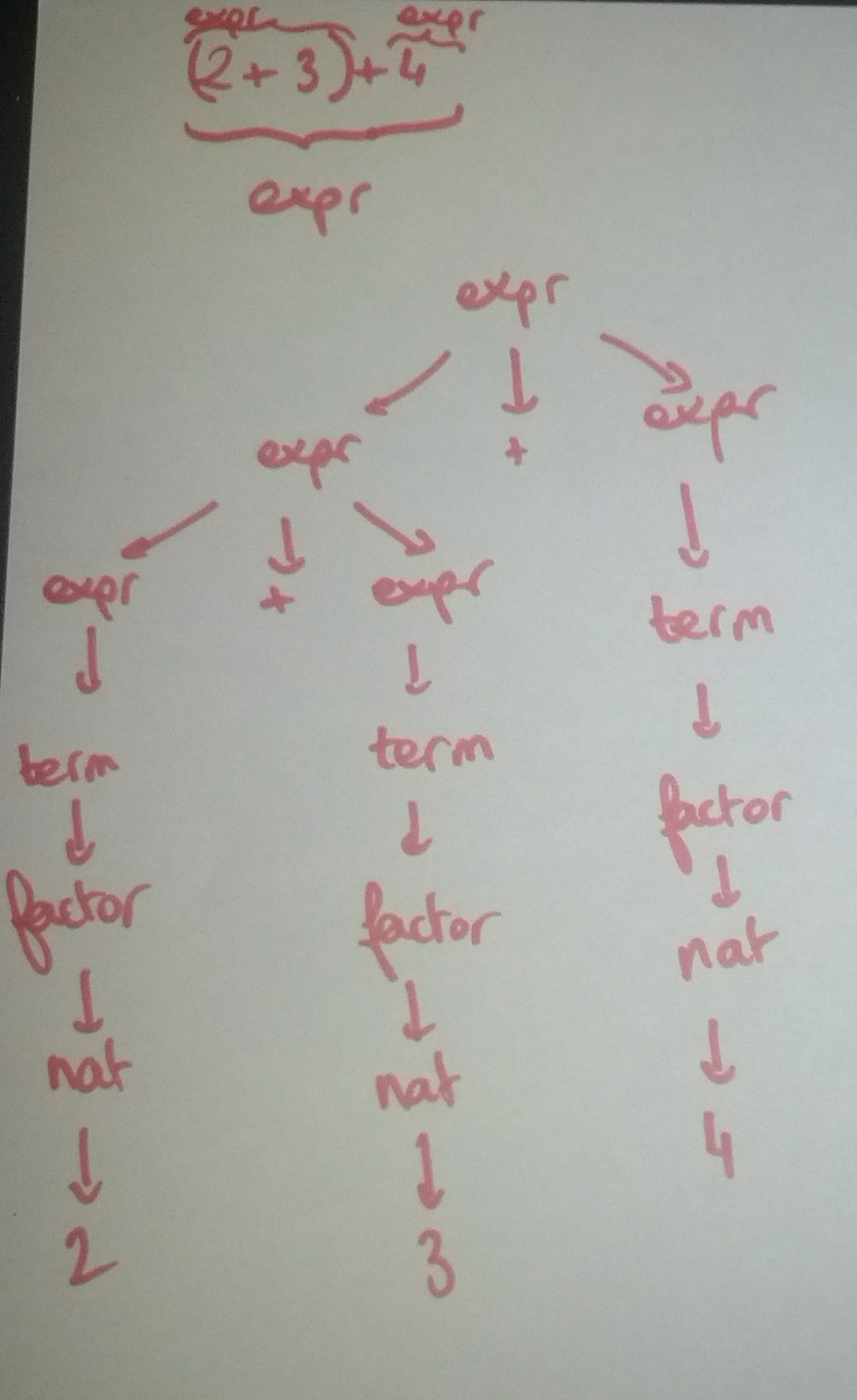
(2+3)+4

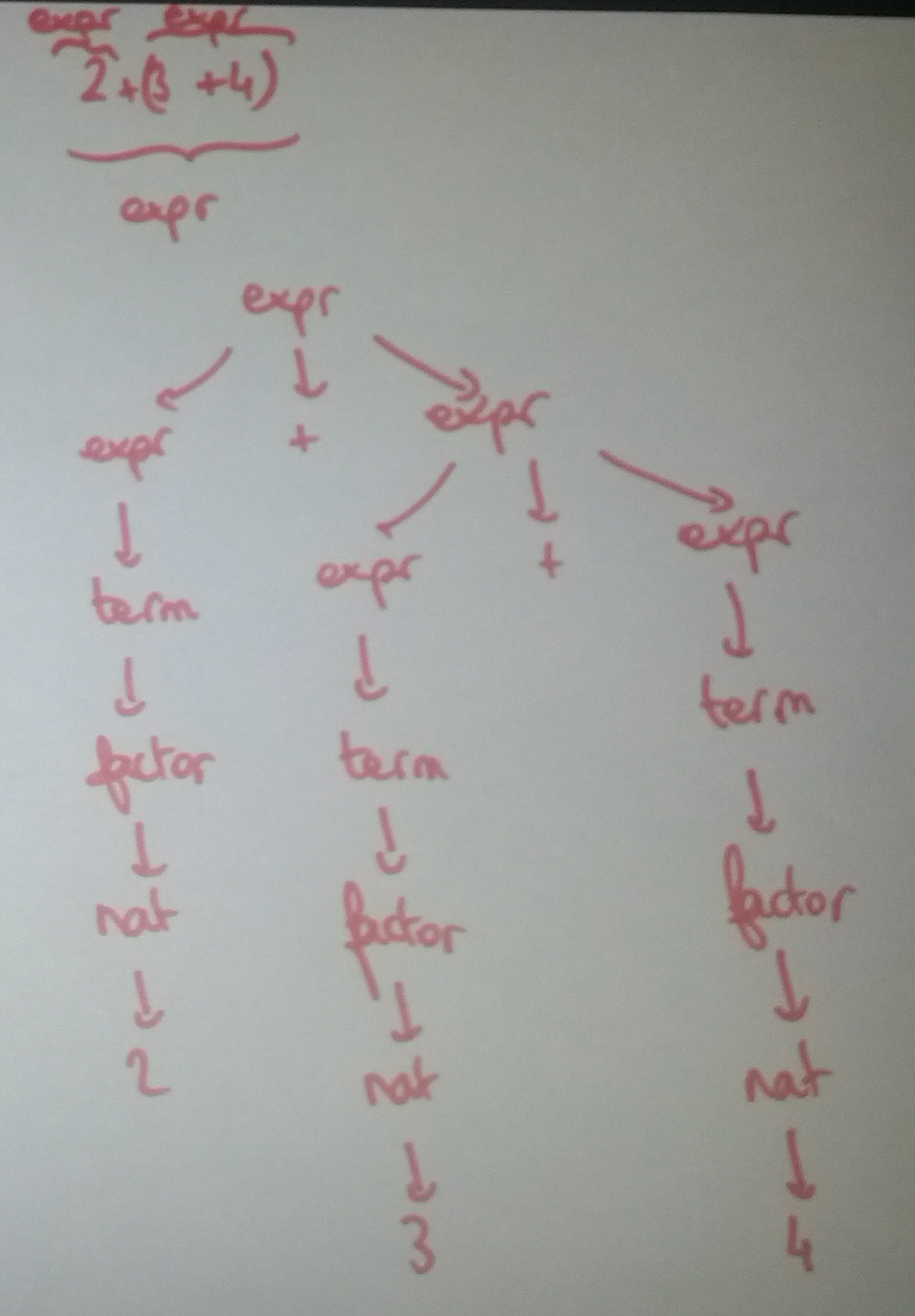
2+(3+4)

Draw Tree 2/2

Using our third grammar for arithmetic expressions, draw the parse trees for the expressions 2 + 3, 2 ∗ 3 ∗ 4 and (2 + 3) + 4.

The grammar:

expr   ::= term (+ expr | epsilon)
term   ::= factor (* term | epsilon)
factor ::= (expr) | nat
nat    ::= 0 | 1 | ... |

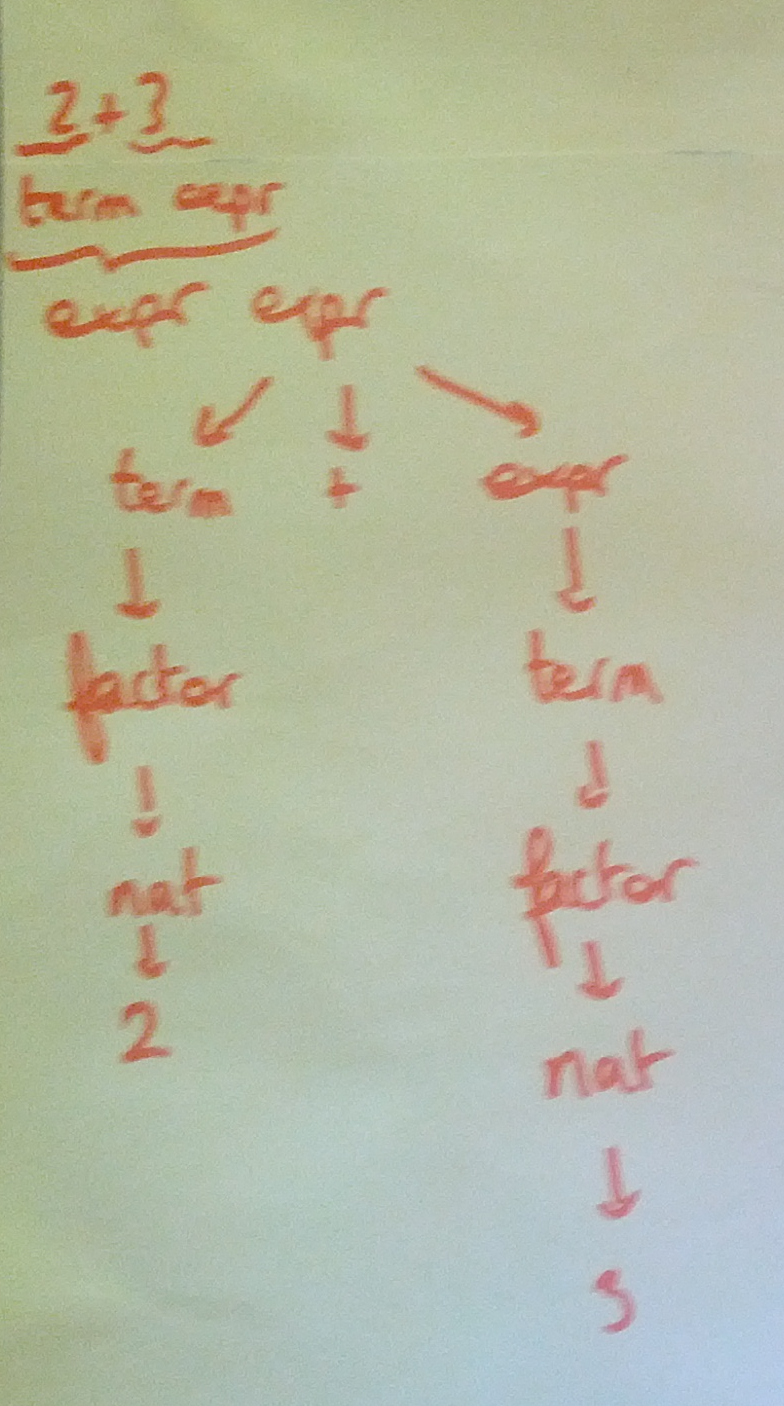
2+3

2*3*4

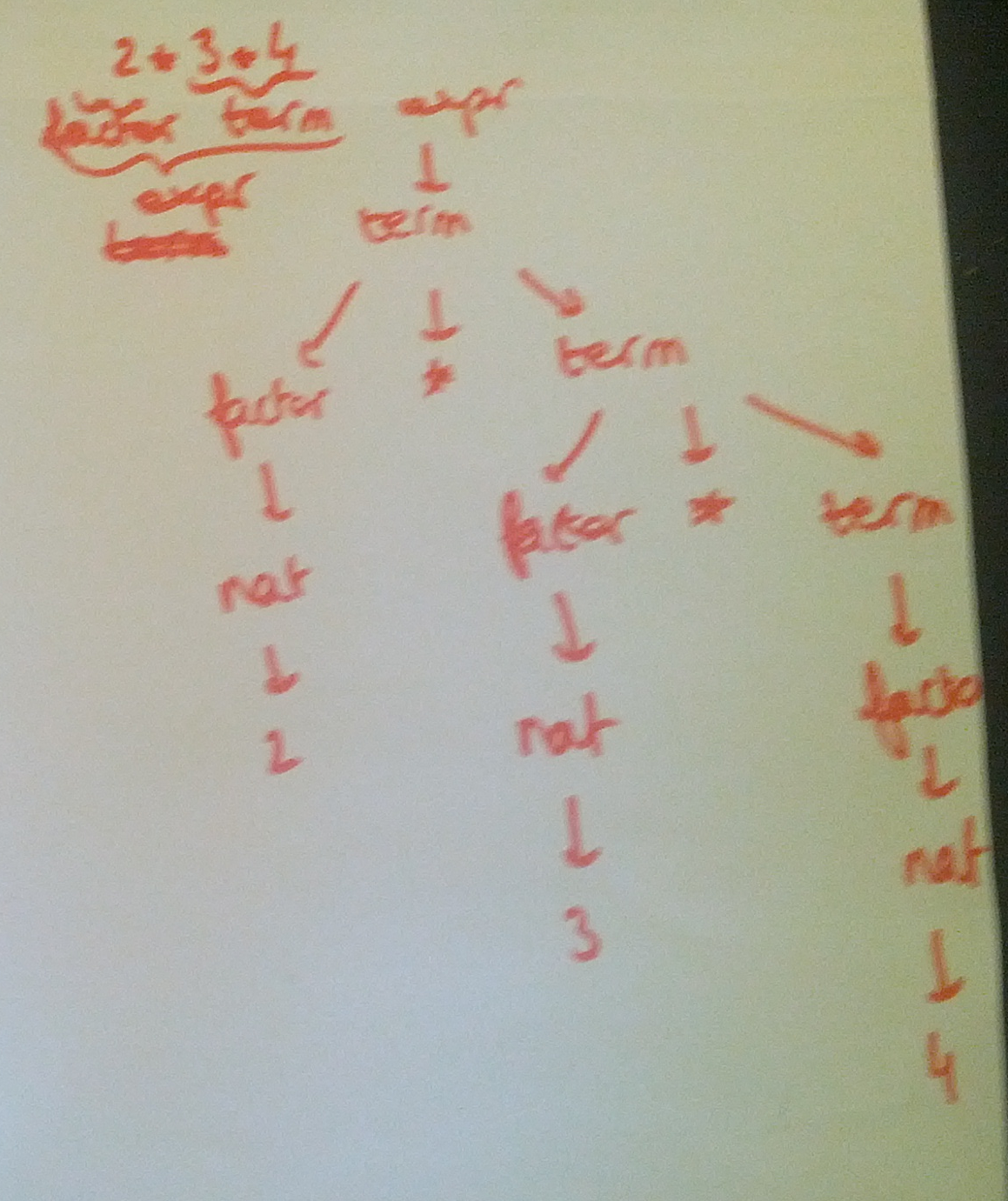
(2+3)*4